報告人: 鄒文明、楊健夫、張建軍
講座日期：2021-07-10
講座時間：08:30—11:50
報告地點：數(shù)學與統(tǒng)計學院學術(shù)交流廳（文津樓3211）
主辦單位：數(shù)學與統(tǒng)計學院 基礎數(shù)學研究中心
講座題目1：變分方法及其對PDE的若干應用
報告人: 鄒文明
講座時間：08:30—09:30
講座內(nèi)容簡介：
先簡要介紹變分法和臨界點理論的歷史。 然后通俗介紹臨界點理論在某些重要的PDE方面的應用，包括對稱擾動方程和Rabinowitz公開問題、Brezis-Nirenberg臨界指數(shù)方程、Li-Lin公開問題、Bose-Einstein凝聚與Sirakov猜想、Lane-Emden方程解的分類、Schrodinger方程的正規(guī)化解等。 同時介紹一些沒有解決的重要問題。
講座人簡介：
鄒文明，清華大學教授，博士生導師。清華大學數(shù)學科學系系主任、中國數(shù)學會常務理事、國家杰出青年基金獲得者、教育部數(shù)學專業(yè)教指委委員，榮獲政府特殊津貼，曾任清華大學基礎數(shù)學研究所所長。目前擔任國際SCI刊物 《中國科學-數(shù)學》、《Minimax Theory and its Application》和《Advances in Nonlinear Analysis》 編委。研究領(lǐng)域主要包括變分與拓撲方法、偏微分方程、Hamiltonian 系統(tǒng)、非線性分析等。在美國Springer-New York出版英文專著二部，發(fā)表SCI論文120余篇，MathSciNet顯示文章被引用2500次。
講座題目2：Improved Sobolev inequalities and critical problems
報告人: 楊健夫
講座時間：9:30—10:30
講座內(nèi)容簡介：
In this paper, we establish two refinement of Sobolev-Hardy inequalities in terms of Morrey spaces. Then, with help of these inequalities, we show the existence of nontrivial solutions for doubly critical problems in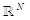 
involving p-Laplacian
,
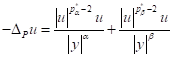Where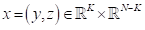
,
,
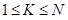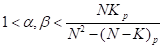and 
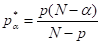is the critical Hardy-Sobolev exponent, and critical problems involving fractional Laplacian
,
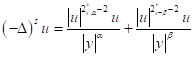where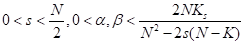 
and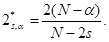 
講座人簡介：
楊健夫，江西師范大學教授，博士生導師。現(xiàn)為《數(shù)學物理學報》常務編委，江西省人民政府學科評議專家，江西省數(shù)學會理事長，國家科學技術(shù)進步獎評審專家，國家基金通訊評審專家，科技部國際合作項目通訊評審專家。1993年起享受國務院特殊津貼，1998年獲國家有突出貢獻中青年專家稱號。先后參加和主持國家科技部重大基礎研究前期研究專項，國家自然科學基金重點項目，國家自然科學基金項目的研究。在國內(nèi)外學術(shù)刊物上發(fā)表近100篇學術(shù)論文。多次應邀赴加拿大、澳大利亞、意大利、瑞典、芬蘭、巴西、智利和香港地區(qū)的高等院校訪問，進行學術(shù)交流。
講座題目3：Ground state solutions of planar Schrodinger-Poisson systems with potential well and lack of symmetry
報告人: 張建軍
講座時間：10:50—11:50
講座內(nèi)容簡介：
In this talk, we are concerned with planar Schrodinger-Poisson systems with nonlinearities having either subcritical or critical exponential growth in the sense of Trudinger-Moser. A feature of this work is that neither the finite steep potential nor the reaction satisfies any symmetry or periodicity hypotheses. The analysis developed in this paper seems to be the first attempt in the study of planar Schrodinger-Poisson systems with lack of symmetry. This is a joint work with Zhisu Liu and Vicenctiu D. Ruadulescu.
講座人簡介：
張建軍，重慶交通大學教授、清華大學博士，美國數(shù)學評論《Mathematics Review》評論員，南開大學陳省身數(shù)學研究所、巴西帕拉伊巴聯(lián)邦大學、意大利因蘇布里亞大學博士后。主持多項國家自然科學基金、意大利倫巴第研究員基金（GLOCAL ERC）、中國博士后科學基金，多項國家自然科學基金等。研究領(lǐng)域主要包括非線分析中的變分與拓撲方法，非線性橢圓方程等，迄今已在包括Comm. PDE, J. Diff. Eqs, J. London Math. Soc., Nonlinearity等刊物上發(fā)表SCI論文40余篇，其中ESI高被引論文4篇。
